
#수 정렬하기2
#합병 정렬
def mergemerge(arr):
if len(arr) <= 1:
print("1자리수인 예외 경우")
return arr
mid = len(arr)//2
mrg = []
print("merge함수 시작",arr)
print("arr[:mid ",arr[:mid],"arr[mid:]",arr[mid:])
left, right = mergemerge(arr[:mid]),mergemerge(arr[mid:])
print("--",left,right)
i,j = 0,0
k =0
while i < len(left) and j < len(right):
print("while문 시작")
k += 1
if left[i] <right[j]:
print("** left {0} < right {1}이므로 ".format(i,j))
mrg.append(left[i])
print("mrg:"+str(mrg[:]))
i += 1
else:
print("** left {0} >= right {1}이므로 ".format(i,j))
mrg.append(right[j])
print("mrg:"+str(mrg[:]))
j += 1
print("while문 횟수,i,j",k,i,j)
if i != len(left):
print("if 문의 i {0} != len(left) {1}".format(i,len(left)))
print(left[i:])
mrg += left[i:]
print("mrg:"+str(mrg[:]))
if j != len(right):
print("if 문의 j {0} != len(left) {1}".format(j,len(right)))
mrg += right[j:]
print("mrg:"+str(mrg[:]))
print("mrg return")
print(mrg)
return mrg
N = int(input())
arr =[]
for i in range(N):
arr.append(int(input()))
answer = mergemerge(arr)
print("answer: ",answer)
def merge_sort(array):
if len(array) <= 1:
return array
mid = len(array) //2
print(array[:mid],array[mid:])
left, right = merge_sort(array[:mid]),merge_sort(array[mid:])
print("left:"+str(left),"right:"+str(right),"mid:"+str(mid))
i,j,k = 0,0,0
while i < len(left) and j < len(right):
if left[i] <right[j]:
array[k] =left[i]
i += 1
else:
array[k] = right[j]
j +=1
k += 1
print("i:",i,"j:",j)
if i == len(left): #한쪽 리스트가 끝난 경우, 나머지 리스트를 넣어줌
while j < len(right):
array[k] = right[j]
j += 1
k += 1
elif j == len(right):
while i < len(left):
array[k] = left[i]
i += 1
k += 1
print("return! array:",array)
return array
n = int(input())
array = []
for _ in range(n):
array.append(int(input()))
array = merge_sort(array)
for data in array:
print(data)병합정렬 개념
분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.

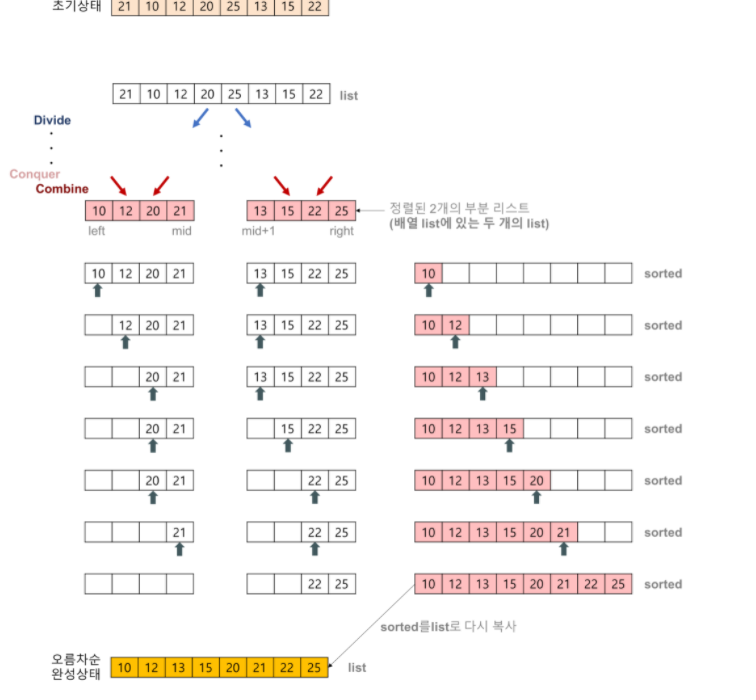
합병 정렬(merge sort) 알고리즘의 개념 요약
‘존 폰 노이만(John von Neumann)’이라는 사람이 제안한 방법
일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬 에 속하며, 분할 정복 알고리즘의 하나 이다.
분할 정복(divide and conquer) 방법
1.문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
2.분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.
과정 설명
1.리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
2.정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
3.각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
4.두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
합병 정렬(merge sort) 알고리즘의 특징
단점
1.만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다.
2.제자리 정렬(in-place sorting)이 아니다.
3.레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.
장점
1.안정적인 정렬 방법
2.데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다. (O(nlog₂n)로 동일)
만약 레코드를 연결 리스트(Linked List)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다.
3.제자리 정렬(in-place sorting)로 구현할 수 있다.
4.따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 졍렬 방법보다 효율적이다.
합병 정렬의 시간 복잡도

레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)임을 알 수 있다.
k=log₂n
각 합병 단계의 비교 연산
크기 1인 부분 배열 2개를 합병하는 데는 최대 2번의 비교 연산이 필요하고, 부분 배열의 쌍이 4개이므로 24=8번의 비교 연산이 필요하다. 다음 단계에서는 크기 2인 부분 배열 2개를 합병하는 데 최대 4번의 비교 연산이 필요하고, 부분 배열의 쌍이 2개이므로 42=8번의 비교 연산이 필요하다. 마지막 단계에서는 크기 4인 부분 배열 2개를 합병하는 데는 최대 8번의 비교 연산이 필요하고, 부분 배열의 쌍이 1개이므로 8*1=8번의 비교 연산이 필요하다. 이것을 일반화하면 하나의 합병 단계에서는 최대 n번의 비교 연산을 수행함을 알 수 있다.
최대 n번
순환 호출의 깊이 만큼의 합병 단계 * 각 합병 단계의 비교 연산 = nlog₂n
이동 횟수
순환 호출의 깊이 (합병 단계의 수)
k=log₂n
각 합병 단계의 이동 연산
임시 배열에 복사했다가 다시 가져와야 되므로 이동 연산은 총 부분 배열에 들어 있는 요소의 개수가 n인 경우, 레코드의 이동이 2n번 발생한다.
순환 호출의 깊이 만큼의 합병 단계 * 각 합병 단계의 이동 연산 = 2nlog₂n
T(n) = nlog₂n(비교) + 2nlog₂n(이동) = 3nlog₂n = O(nlog₂n)
'IT' 카테고리의 다른 글
| 파이썬 2차원 배열 선언 이해하기 (깊은 복사 얕은 복사) (0) | 2022.04.27 |
|---|---|
| 좋은 객체 지향 프로그래밍이란(feat.배달의 민족 김영한) (0) | 2022.03.24 |
| 시간복잡도 개념 정리 (0) | 2022.02.25 |
| C언어 오류 [Run-Time Check Failure #2] (0) | 2021.09.03 |
| C언어 백준 4673번 셀프넘버 해설 (0) | 2021.09.01 |