문제
도현이의 집 N개가 수직선 위에 있다. 각각의 집의 좌표는 x1, ..., xN이고, 집 여러개가 같은 좌표를 가지는 일은 없다.
도현이는 언제 어디서나 와이파이를 즐기기 위해서 집에 공유기 C개를 설치하려고 한다. 최대한 많은 곳에서 와이파이를 사용하려고 하기 때문에, 한 집에는 공유기를 하나만 설치할 수 있고, 가장 인접한 두 공유기 사이의 거리를 가능한 크게 하여 설치하려고 한다.
C개의 공유기를 N개의 집에 적당히 설치해서, 가장 인접한 두 공유기 사이의 거리를 최대로 하는 프로그램을 작성하시오.
정답코드
# 공유기 설치
from array import array
import sys
N,C = map(int,input().split())
answer = 0
location_list = []
for i in range(N):
location_list.append(int(sys.stdin.readline().rstrip()))
#정렬하기 for 이분 탐색
location_list = sorted(location_list)
def Binary(start, end):
global answer
if start > end:
return
count = 1
mid = (start + end) // 2
current = location_list[0]
for i in range(1,len(location_list)):
if location_list[i] - current >= mid:
count += 1
current = location_list[i]
if count < C: # 개수가 적으면 값을 줄여야 하므로
return Binary(start, mid -1)
else:
answer = mid
return Binary(mid+1, end)
Binary(1, location_list[-1] - location_list[0])
print(answer)
풀이
어떻게 접근해야할지 어떻게 이분탐색을 적용할지 몰라 헷갈렸던 문제이다. 아마 나와같은 이분탐색 초보들은 헷갈렸을 것같다. 두 공유기 사이 길이 차이가 일정하지 않으니(1,4 vs 4,8 은 각각 3과 4로 값이 다르다.) 따라서 특정한 값을 구한다는 이분 탐색을 어떻게 활용할지 도무지 감이 오지 않았다. 하지만 이 문제는 이분탐색으로 특정 값을 구해 풀 수 있다.
for i in range(1,len(location_list)):
if location_list[i] - current >= mid:
count += 1
current = location_list[i]위와 같은 코드를 통해 특정값을 기준으로 하지만, 길이 차이가 일정하지 않아 여러 값(각각 3과 4)을 고려해야하는 딜레마를 해결할 수 있게 되었다. 사실 생각해보면 값의 차이가 3이든 4이든 사이의 거리가 특정 값보다 같거나 크면 되는 것이기 때문에 저런 코드를 작성하면 되는 것이었다.
우리는 기준 값을 구하고 각각의 원소들을 비교하면서 거리가 기준 값보다 크거나 같은 것들의 개수를 세는 알고리즘을 작성하는 것이다.

예제 입력1에서 만약 조건을 만족하는 것이 C보다 작다면?
예를 들어 mid 가 4일 때 count = 2 이다 ([1, 2, 4, 8, 9])
이런 경우 count를 늘리려면 어떻게 해야할까?
mid 값 (기준) 을 줄여야 한다. 이분 탐색에서 우리는 값을 줄이기 위해 왼쪽 구간을 탐색했다. 따라서 start, mid -1 구간의 탐색을 시도하게 되는 것이다. 이런식으로 가능한 mid의 값을 탐색해 나가는 것이다.
이분탐색이 복잡해 보이지만 사실 단순하게 보면 이거보다 큰값을 넣을까 작은 값을 넣을까? 의 문제일 뿐이다.
Q) mid = 2일때도 값이 성립하는데 어떻게 mid = 3을 값으로 도출할 수 있는가?
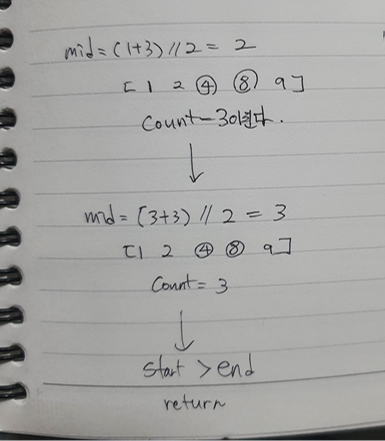
특정 범위 내의 값이 성립했다고 해도 우리는 최대 값을 구하는 것이 목표이다.
else:
answer = mid
return Binary(mid+1, end)else 문의 조건을 떠올려보자. 여기엔 같을 때라는 조건도 포함된다. 즉 mid = 2 일 때 C == count로 조건을 만족하므로 다시 이분 탐색을 하게된다. 여기서 범위에 주목해보자 (mid +1, end) 이다. 이는 직전의 범위과 끝점은 같게 고정시키고, 다시 그것보단 큰 수를 이분탐색한다는 것을 의미한다. 생각해봤을 때, 특정 값이 조건을 만족한다고 할지라도 최대값을 구하기 위해선, 범위내에서 조건을 만족하는 것보다 더 큰 수들도 체크해봐야한다.
배운점 && 공부방향
1. 이분탐색은 어떤 특정한 값을 효율적으로 도출하는 방법일 뿐이다. 다른 것들과 헷갈리지 말자.
'CS > 알고리즘' 카테고리의 다른 글
| 파이썬 백준 14501번 퇴사 풀이( 여러가지 방법으로 풀기) (0) | 2022.05.09 |
|---|---|
| 백준 1300번 K번째 수 파이썬 풀이 (0) | 2022.04.28 |
| 백준 1654번 랜선 자르기 파이썬 풀이(feat. 메모리 초과 해결) (0) | 2022.04.25 |
| 이진 탐색 알고리즘에 대해 알아보자 (0) | 2022.04.24 |
| 백준 5430번 AC 파이썬 풀이 (시간초과 해결) (0) | 2022.04.18 |