백준 11401번 이항계수3 파이썬 풀이
문제
자연수 n과 정수 k가 주어졌을 때 이항 계수 nCk를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
선제적으로 알고 있어야하는 개념
역원
그 수와 곱하면 곱셈 항등원(1)이 되는 수
모듈로 연산(Modulo Operation)
어떤 한 숫자를 다른 숫자로 나눈 나머지를 구하는 연산으로, 나머지 연산(mod)이라고 한다.
ex) 18 (mod 5) = 3
ex) 7²²² mod 11 계산하기
7¹¹-¹ = 1(mod 11)
7¹⁰ = 1(mod 11)
7²²² = 7²²*¹⁰ x 7² (mod 11)
= 49(mod 11)
= 5(mod 11)
페르마의 소정리
p가 소수이고 a가 정수라고 할 때 p에서 a^p와 a는 서로 합동이다.

이를 양변을 약분하여 아래와 같이 쓸 수 있다.

나머지(Modulo) 연산 분배법칙
(A + B) % p = ((A % p) + (B % p)) % p
(A * B) % p = ((A % p) * (B % p)) % p
(A - B) % p = ((A % p) - (B % p) + p) % p
풀이과정
편의상 1,000,000,007을 p라 하고, 이를 다시 공식으로 써 보면
모듈러 연산은 분수에 적용할 수 없다. 따라서 문제에서 p의 역원을 구해야함.
이 문제는 나머지 연산 분배법칙을 활용 + 이를 위해 페르마의 소정리를 활용 하는 방식으로 문제를 해결해야한다.
(A / B) % p = (A * B^(p-2)) % p = ((A % p) * (B^(p-2) % p)) % p
모듈러 연산은 분수에 적용할 수 없다. 따라서
위의 식을 계산하기 위해선 k!(n-k)!%p의 역원을 구해야한다.
역원을 구하는 이유 -> k!(n-k)!가 분모에 있기 때문에 나머지 연산 분배법칙 활용 불가.
p가 소수이고 a가 p의 배수가 아니면 아래의 식이 성립한다.

이를 변형하면 다음과 같다.

즉, (k!(n-k)!)-1 % p = (k!(n-k)!)^p-2 % p (mod p) 가 된다.
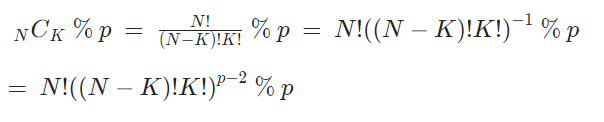
정답코드
n, k = map(int,input().split())
P = 1000000007
def factorial(num, mod):
result = 1
for i in range(2, num+1):
result = result * i % P
return result
def power(num, p, mod):
if p == 1:
return num % mod
if p % 2:
return ((power(num,p//2,mod) ** 2) * num) % mod
else:
return (power(num,p//2,mod) ** 2) % mod
# 분할 정복은 이 거듭제곱에서 활용된다.
print(factorial(n, P) * power((factorial(k, P) * factorial(n-k, P)), P-2, P) % P)
Q) 왜 print할 때 %P가 추가가 되나요??
((N!)((N-k)!K!)-¹)%P
=(N!)%P * ((N-K)!K!)-¹ %P %P ( 분배법칙활용)
= factorial(n, P) *(factorial(k, P) * factorial(n-k, P))-¹% P
배운점 && 공부방향
1. 곱셈과 덧셈 뺄셈 등으로 만 이루어진 식은 계속 나눠도 나머지가 같다.
100 % 11 = ((1 % 11) *(5 % 11) * (10 %11) * (2 % 11))%11
2. 오버플로우를 방지하기위해 아래와 같은 식을 활용한다. (1의 원리에 의해)
def factorial(num, mod):
result = 1
for i in range(2, num+1):
result = result * i % P
return result
'CS > 알고리즘' 카테고리의 다른 글
| 백준 5430번 AC 파이썬 풀이 (시간초과 해결) (0) | 2022.04.18 |
|---|---|
| 알고리즘 구현 실수 유형 정리 (0) | 2022.04.15 |
| 백준 17298 오큰수 파이썬 풀이 시간초과 해결 (0) | 2022.04.07 |
| 백준 4949 균형 잡힌 세상 파이썬 풀이 (0) | 2022.04.05 |
| 백준 1707번 이분 그래프 파이썬 풀이 (0) | 2022.04.04 |